polynomial regression 사용해보기 (with js)

회사 일 중에 시간별 수량 값을 그래프로 시각화 할 일이 생겼다.

뭐 어찌저찌 열심히 코드 짜서 (d3+c3 chart 이용) 그래프를 그렸더니

 

(예측 선 + 신뢰구간 추정)도 존재했으면 좋겠다! 라고 위에서 요청이 와서 다시 수정...

일단 잘 모르니 구글에 검색해보자... 추세 예측...

어,,,음,,,,

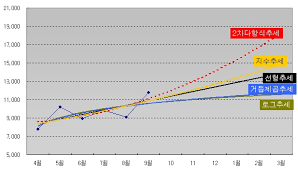
1. 예측 선

 

forecast 방법을 찾아보니 선형회귀 방법을 쓰라고 나온다. 

선형회귀라 하면 학부생 2학년때 파이썬 처음 배우면서 배웠던 기억이 있는데 정확히 기억은 안나고,

코드 따라치면서 왜 배우는지 모르겠다 욕했던 것만 기억난다.

 

각설하고 간단하게 선형회귀는

기존 기간의 값이 이랬으니 -> 새로운 기간의 값은 이럴 것이다. 라고 새로운 값을 추측하기 위해 쓴다고 한다...

더 자세한 설명은 https://knowing207.tistory.com/20

Chapter 3. 선형회귀 (Linear Regression) - 1) 단순선형회귀

 

나타난 데이터를 통해 데이터를 표현할 수 있는 방정식을 찾는 과정이라고 말할 수 있다.

선형이라는 말은 방정식으로 1차 방정식 (ex. y = ax + b) 을 사용하기 때문에 선형이라고 이름 붙었다.

결과물에 맞는 방정식을 찾기 위해 a와 b를 찾는 것이라고 할 수 있겠다.

 

a와 b는 방정식과 실제 데이터간의 간극(혹은 데이터와 방정식의 결과 간의 차이 = 오차라고 표현)

이 최대한 작게끔 만들어 방정식이 데이터를 잘 표현하게끔 만들어야 하는데

이때 사용되는 오차 값 표현을 최소 제곱법을 이용해 표현한다.

 

찾다보니 자꾸 엑셀 함수 알려주는 글들이 많아 들어가서 몇개보니

https://suninara.tistory.com/entry/%EC%97%91%EC%85%80-%ED%86%B5%EA%B3%84%ED%95%A8%EC%88%98-FORECAST-%ED%95%A8%EC%88%98-%EB%8B%A8%EC%88%9C%EC%84%A0%ED%98%95%ED%9A%8C%EA%B7%80-%EC%98%88%EC%B8%A1%EA%B0%92%EC%9C%BC%EB%A1%9C-%EB%AF%B8%EB%9E%98%EC%9D%98-%ED%8C%90%EB%A7%A4%EB%9F%89-%EA%B5%AC%ED%95%98%EA%B8%B0

엑셀 통계함수 FORECAST 함수 단순선형회귀 예측값으로 미래의 판매량 구하기

 

오히려 머신러닝 소개 블로그보다 쉽게 써놓은것 같아 가져와봤다. 위 두개 블로그를 통해 a,b를 보자면

a = (x,y 공분산) / (x 분산)

b = y_avg - a * x_avg

 

이라고 한다.

하지만 나는 직선 방정식이 아닌 곡선이 필요했다. 

곡선이 되려면 1차보다 다차의 방정식을 만들어야 하고 좀더 구글링 해보자.

 

1차 이상의 선형회귀를 다항 회귀라고 부른다. (polynomial regression)

하지만 다항회귀의 경우, a,b가 아닌 

b1,b2,b3...등 각 항에 맞는 값들을 구하기 위한 계산이 늘어난다.

이런 방정식을 만들기 위해서...

이런 방정식이 필요하다...

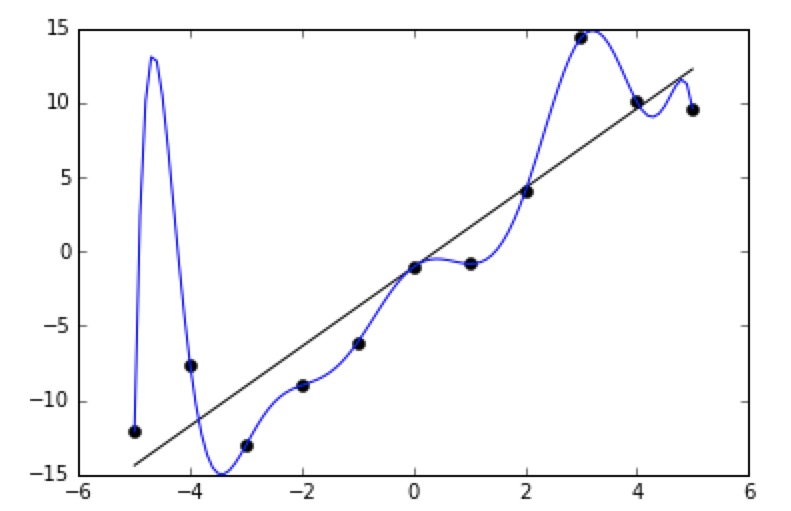
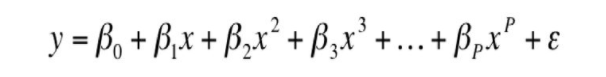
내가 구현할 수 있는가? 답은 no...

당장 그래프에 추가해야하는데 모듈을 구성할 내 실력이 안되는 안타까운 상황

그래서 이미 잘나온 모듈을 구해서 사용해보자

https://github.com/Tom-Alexander/regression-js

Tom-Alexander/regression-js

해당 모듈을 이용하면

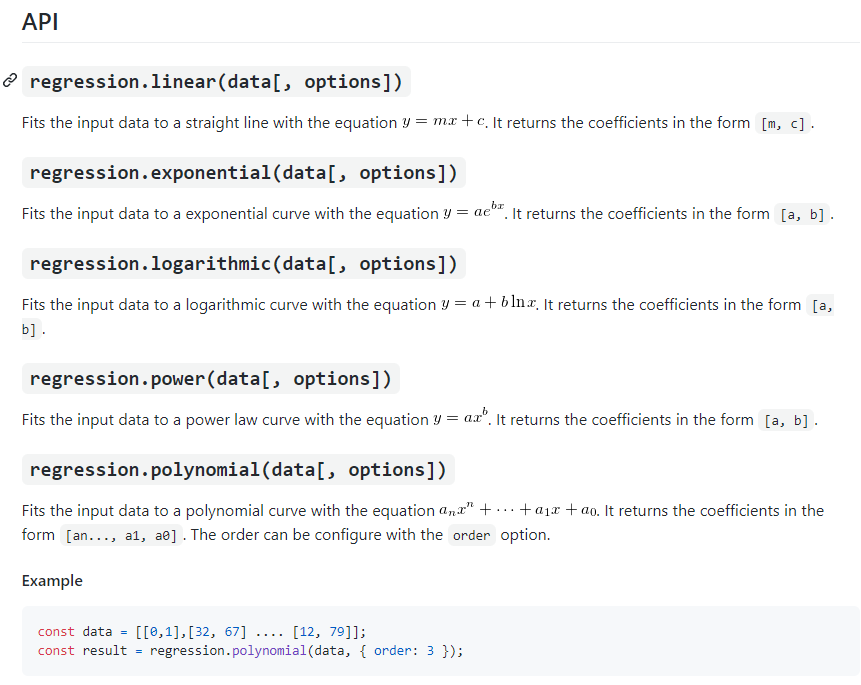
이런식으로 쉽게 함수 호출로 결과값을 뽑아낼 수 있게 된다.

 

2. 신뢰구간

 

역시 잘모르니 구글을 통해 찾아보자

https://otexts.com/fppkr/prediction-intervals.html

Forecasting: Principles and Practice (2nd ed)

찾아온 링크의 본문에 의하면

신뢰구간 +/-95% 추정은 (예측 단계 +/- 예측단계의 표준편차 * 1.96) 을 통해 구할 수 있다고 되어 있다.

산 넘어 산이다. 나는 통계를 아예 모르기 때문에 표준편차가 뭔지 또 찾아봤다.

 

표준편차란?
- 평균 = 각 변량의 합 / 각 변량의 개수
- 편차 = 각 변량에서 전체 평균을 뺀값
- 분산 = 편차의 제곱의 합을 변량의 개수로 나눈 값
- 표준 편차 = 분산의 제곱근

 

글로 풀어보니 저정도는 코드로 짜서 사용할 수 있겠다 싶었다.

그래도 혹시 모르니 손으로 먼저 계산해보자 싶어

https://www.rapidtables.org/ko/calc/math/standard-deviation-calculator.html

표준 편차 계산기 (σ)

계산기의 도움을 빌려 내가 계산한 값과 실제로 표준변차 계산이 일치하는지 검사해봤었다.

새로운 값 y1 이라 하자
  - y1 +/- 1.96 * 표준편차
  - y1 = 16,

   평균 = 16 / 1,

   편차 = (16 - 16) /1,

   분산 = 0^2 / 1,  

   표준편차 = ( 0 ) ^ 1/2 = 0
   신뢰구간 = (16 +/- 1.96*0) = [16, 16]

새로운 값 y2 = 17 추가시
  - y2 +/- 1.96 * 표준편차
  - y2 = 17,

   평균 = 16 + 17 / 2,

   분산 = ( (16-16.5)^2 + (17-16.5)^2 ) / 2 ,

   표준편차 = (0.25) ^ (1/2) = 0.5
   신뢰구간 = (17 +/- 1.96*0.5) = [16.02,17.98]

 

계산기 값과 손으로 계산한게 동일했다. 이제 고대로 코딩으로 옮기면 된다.

 

3. 구현

 

구현은 js로 구현했었다. 위에 찾은 모듈도 javascript 였고, 보여주는게 다였기 때문에

먼저 js code로 보자

 

신뢰구간 계산 함수

function confidence_interval(current_num, num_list){
    var mean = 0 // 평균
    for(var i = 0; i < num_list.length; i++){
        mean+= num_list[i];
    }
    mean = mean/ num_list.length;
    
    var varience = 0; // 분산
    for(var i = 0; i < num_list.length; i++){
        varience += Math.pow((num_list[i] - mean),2);
    }
    varience = varience / num_list.length;
    
    var standard = Math.sqrt(varience); //표준편차
    
    var plus = current_num + (1.96 * standard); //신뢰구간 +95%
    if(plus < 0)
        plus = 0
    var minus = current_num - (1.96 * standard); //신뢰구간 -95%
    if(minus < 0)
        minus = 0
        
    var confidence = []
    confidence.push(minus)
    confidence.push(plus);
    
    return confidence;
}

예측치 계산의 경우 로직을 먼저 설명하자면

1. 어제 날짜의 값을 통해 다항회귀를 이용, n차 방정식을 만든다 (정확히는 각 항의 계수값을 계산)

데이터 형식은 [ [0, 값], [1,값], [2,값], ...] 으로 x는 단순 숫자의 증가, y는 실제 관측치

n차의 경우 over-fitting이 되어도 괜찮으니 최대한 값이 데이터를 반영하도록 데이터의 개수와 동일하게 맞추기

// historyIndex => 데이터
// historyIndex.length => 데이터 개수 이자 n차 방정식의 n을 지정
var polyReg = regression('polynomial', historyIndex, historyIndex.length);

// 결과로는 각 항의 계수값 반환

 

2. 예측이 필요한 값(y_hat) 을 구하기 위해 x값을 대입

var val = i; // x값 (0,1,2,3...등 단순 숫자 증감)
var value = 0;
var polyReg = regression('polynomial', historyIndex,historyIndex.length); // today_predict.length

for(var j = polyReg.equation.length-1; j > -1; j--){
	value += polyReg.equation[j] * Math.pow(val, j);
} // y = a + b1x^1 + b2x^2 + ...의 식을 나타냄

if(volume < 0) // 방정식과 달리 수량값은 - 값이 존재할수 없기때문에
	volume = 0;

 

3. 예측값들로 상한/ 하한 값을 반환

num_list.push(value); // 예측값을 계속 추가
var confidence = confidence_interval(value, num_list); // 앞서 만든 신뢰구간 함수 사용

 

4. 방정식을 만들기 위한 이전 데이터중 맨앞 제거, 새로운 예측치 추가 (Queue처럼 데이터 하나 빼고, 하나 추가)

historyIndex = historyIndex.slice(1, historyIndex.length); // 맨앞제거
historyIndex.push([val, value]); // 맨뒤 추가

5. 1-4 반복

today_predict = today_predict.map((d, i) => {
        var val = i; 
        var value = 0;
        var polyReg = regression('polynomial', historyIndex,historyIndex.length); // today_predict.length
        for(var j = polyReg.equation.length-1; j > -1; j--){
            value += polyReg.equation[j] * Math.pow(val, j);
        }
        
        if(value < 0)
            value = 0;
        
        num_list.push(value);
        
        var confidence = confidence_interval(value, num_list);
        
        historyIndex = historyIndex.slice(1, historyIndex.length);
        historyIndex.push([val, value]);
    return {
            minus : parseInt(confidence[0]),
            plus : parseInt(confidence[1]),
            volume: parseInt(value),
        }
    });

 

위 식으로 그래프를 그리면 어떻게 나오는지 보자

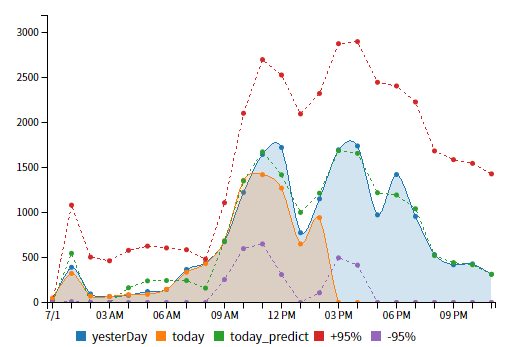
파란색 = 어제 날짜 수량값

주황색 = 오늘 날짜 수량값

초록 점선 = 오늘의 예측치

빨강/보라 = 예측치를 통한 상한/하한 (신뢰구간 95%)

 

나름 이쁘게 그려지는걸 확인 할 수 있다.

 

 

4. 느낀점

아쉬운점은 다항회귀 이렇게 쓰는건지 잘 모르겠다...? 정도

이렇게 쓰는게 맞는건가???

개발자 실격???