등수 반환 문제 고찰

Q. 성적이 입력되고 그 학생의 등수를 출력하는 함수를 작성하시오.

점수는 0~100이고, 점수는 랜덤으로 들어온다. rank 함수는 20억 회 이하로 동작된다.(대충 이런 내용)

전역변수, 클래스 등 자율적으로 사용해도 무관.

시간과 메모리 등을 고려하여 작성

ex. 1번째: Score: 70 -> return 1

2번째: Score: 100 -> return 1

3번째: Score: 80 -> return 2

4번째: Score: 70 -> return 4

5번째: Score: 50 -> return 5

 

문제 출처 : https://okky.kr/articles/1052166

 

문제 해결을 위한 rank 계산 코드 짜기

 

version 1.

첫번째 접근 → 단순히 리스트에 넣고, 정렬하고, 해당 숫자 찾아서 알려주자~

order = []

nums = [70,100,80,70,50]
for num in nums:
    order.append(num)
    order = sorted(order)
    index = order.index(num)
    print("num : {}, order : {}".format(num, len(order)-index))
    
"""
num : 70, order : 1
num : 100, order : 1
num : 80, order : 2
num : 70, order : 4
num : 50, order : 5
"""

 

 

version 2. 

리스트에 넣을 때, 넣을 자리를 찾아서 넣자 그럼 정렬 필요 없잖아! 그리고 그 자리가 그 점수의 등수닷!

def binSearch(target, num_list):
    l = 0
    r = len(num_list)
    while l < r:
        m = (l+r) // 2
        if num_list[m] == target:
            return m
        else:
            if num_list[m] < target:
                l = m+1
            else:
                r = m
    return l

nums = [70,100,80,70,50]
order = []
for num in nums:
    index = binSearch(target = num, num_list = order)
    order.insert(index, num)
    print("num : {}, order : {}".format(num, len(order)-index))
    
    
"""
출력결과
num : 70, order : 1
num : 100, order : 1
num : 80, order : 2
num : 70, order : 4
num : 50, order : 5
"""

 

version 3.

점수는 0~100까지로 정해져있다. 100칸만 만들고 개수 합산만 진행하자!

scores = [0 for _ in range(101)] # 0~100

nums = [70,100,80,70,50]
for num in nums:
    scores[num] += 1
    order = 0
    for score in range(100, num-1, -1):
          order += scores[score]
    print("num : {}, order : {}".format(num, order))
    
    
"""
출력결과
num : 70, order : 1
num : 100, order : 1
num : 80, order : 2
num : 70, order : 4
num : 50, order : 5
"""

 

이 세가지의 다른 해결 방안이 도출될 수 있다. 물론 1부터 3까지는 각 단계의 단점을 조금씩 보완했는데

실제로 시간 측정, 메모리 소요 등으로 비교해서 결과는 어떤지 어떤 점을 보완한 건지 살펴보자.

 

일단 해당 함수들을 통합하자

class rankCalculate:
    def __init__(self):
        self.order = []
        self.scores = [0 for _ in range(101)] # 0~100
        
    def rank_1(self, num):
        self.order.append(num)
        self.order = sorted(self.order)
        index = self.order.index(num)
        print("num : {}, order : {}".format(num, len(self.order)-index))
    
    def rank_2(self, num):
        def binSearch(target, num_list):
            l = 0
            r = len(num_list)
            while l < r:
                m = (l+r) // 2
                if num_list[m] == target:
                    return m
                else:
                    if num_list[m] < target:
                        l = m+1
                    else:
                        r = m
            return l
        index = binSearch(target = num, num_list = self.order)
        self.order.insert(index, num)
        print("num : {}, order : {}".format(num, len(self.order)-index))
    
    def rank_3(self, num):
        self.scores[num] += 1
        order = 0
        for score in range(100, num-1, -1):
            order += scores[score]
        print("num : {}, order : {}".format(num, order))

 

각 버전 별 시간, 메모리 계산 테스트

 

시간 측정 결과!

n번씩 수행할 때, 아래와 같다.

n = 10000
test#1 0.25726 sec
test#2 0.01301 sec
test#3 0.01599 sec

n = 100000
test#1 26.71987 sec
test#2 0.49301 sec
test#3 0.16026 sec

n = 1000000
test#1 3762.05481 sec
test#2 62.82765 sec
test#3 1.70616 sec

 

시간 복잡도의 경우,

단순한 rank_1 메서드는 점수값을 마지막에 추가하고 sort → 해당 숫자를 찾고 반환!!

넣고(O(1)), 정렬하고(O(nlogn)), 숫자를 찾기 O(n)

위 작업을 반복하다보니 엄청나게 오래 걸리게 된다.

 

두 번째 rank_2 메서드의 경우,

넣어야 할 부분을 찾고 해당 부분에 넣는다는 점에서 rank_1의 O(n) 수행시간을 줄였다는 장점이 있다.

그렇기에 정렬 부분이 필요 없다! 하지만 넣는 양이 증가함에 따라 list 자료구조의 치명적인 단점이 있는데

만약 삽입을 하다 모자른다? → 새 배열 선언해 값 통째로! 복사가 일어난다!!

그렇기 때문에 O(n)의 시간이 걸린다!!

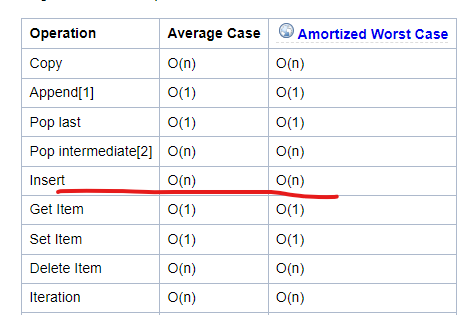
정리하면, 찾아서(binary search O(logn)) → 넣기 (O(n)) 의 시간만큼 걸리기 때문에

rank_1보다는 줄였지만 여전히 꽤 오래 걸리는 걸 확인할 수 있다.

(게다가 binSearch 함수를 호출할때마다 선언하니 더더욱 느릴 수밖에…!)

 

세 번째 메서드인 rank_3의 경우

각 점수별 index로 접근해 배열 값을 +1 한다. (위 insert 작업을 대신)

index로 접근했기에 O(1)이고, 등수를 구하기 위해 점수값보다 큰 점수들의 개수를 조회하는데

아무리 길어도 100~0까지밖에 반복을 안 하기 때문에 시간도 짧다.

정리하면, 찾아서 넣기 (O(1)) → 등수 반환하기 (O(100) → O(1)) 이기 때문에

속도측정면에서도 굉장히 빠르게 나오는 걸 확인할 수 있다.

 

 

메모리의 경우는 간단한데 단순히 생각해 봐도

rank_1, rank_2 메서드의 경우는 값이 들어오는 대로 배열에 추가하기 때문에

n개만큼의 메모리를 차지하게 된다. O(n)의 크기!!

rank_3 메서드의 경우는 처음 선언 시 0~100까지의 101개의 배열을 이미 선언하고

이 배열만큼만 사용하기 때문에 O(1)이라고 할 수 있다.

 

시간, 공간의 단점을 다 극복한 최적의 방법은 rank_3!

 

이렇게 한 개의 문제를 가지고 여러 방법으로 풀 수 있다는 점이 즐겁다.

게다가 작년에 나에 비해 이렇게 다방면으로 문제 풀이를 할 수 있다는 점도 새롭게 다가왔다.

 

그렇지만… 프로그래머로써 어려운 점이 있다면…

어떤 문제나 실제 상황에서 풀 때 느끼는 “분명 최적화된 방법이 존재할 것 같다”는 그 은은한 불안감 때문 아닐까?

(근데 나는 그런 거 잘 못함)